Образец решения системы уравнений
Способ подстановки в решении систем уравнений
Системой линейных уравнений с двумя неизвестными - это два или несколько линейных уравнений, для которых необходимо найти все их общие решения. Мы будем рассматривать системы из двух линейных уравнений с двумя неизвестными. Общий вид системы из двух линейных уравнений с двумя неизвестными представлен на рисунке ниже:
< a1*x + b1*y = c1,
< a2*x + b2*y = c2
Здесь х и у неизвестные переменные, a1,a2,b1,b2,с1,с2 - некоторые вещественные числа. Решением системы двух линейных уравнений с двумя неизвестными называют пару чисел (x,y) такую, что если подставить эти числа в уравнения системы, то каждое из уравнений системы обращается в верное равенство. Рассмотри один из способов решения системы линейных уравнений, а именно способ подстановки.
Алгоритм решения способом подстановки
Алгоритм решения системы линейных уравнений способом подстановки:
1. Выбрать одно уравнение (лучше выбирать то, где числа меньше) и выразить из него одну переменную через другую, например, x через y. (можно и y через x).
2. Полученное выражение подставить вместо соответствующей переменной в другое уравнение. Таким образом, у нас получится линейное уравнение с одной неизвестной.
3. Решаем полученное линейное уравнение и получаем решение.
4. Подставляем полученное решение в выражение, полученное в первом пункте, получаем вторую неизвестную из решения.
5. Выполнить проверку полученного решения.
Пример
Для того, чтобы было более понятно, решим небольшой пример.
Пример 1. Решить систему уравнений:
<2*x-3*y=-18 1. Из первого уравнения данной системы выражаем переменную х. Имеем x= (12 -2*y) 2. Подставляем это выражение во второе уравнение, получаем 2*x-3*y=-18 2*(12 -2*y) - 3*y = -18 24 - 4y - 3*y = -18 4. Подставляем полученный результат в выражение, полученное в первом пункте. x= (12 -2*y) x=12-2*6 = 0 x=0 5. Проверяем полученное решение, для этого подставляем найденные числа в исходную систему. Здесь приводится пример решения системы линейных уравнений методом Гаусса с помощью программы онлайн на сайте решения задач по математике http://kontrolnaya-rabota.ru Допустим нам дана линейная система уравнений такая: Заходим на страницу сервиса Решение системы линейных уравнений методом Гаусса онлайн Указываем размер вводимой системы уравнений так: Или так: После того, как ввели количество решаемых уравнений, вводим коэффициенты при неизвестных в уравнении: Осталось сделать почти ничего - переписать нужный ход решения (выбирая нужное), а также написать решение. Отсюда у нас должно получиться Вот такой результат: Внимание! Если оставшихся коэффициентов в каждой строке больше чем 1, то скорее всего решений бесконечно много Так же может получится, что нет вообще ни одного решения. Пож. проверяйте! Опубликовано: Январь 7, 2011 На данном уроке мы рассмотрим методы решения системы линейных уравнений. В курсе высшей математики системы линейных уравнений требуется решать как в виде отдельных заданий, например, «Решить систему по формулам Крамера», так и в ходе решения остальных задач. С системами линейных уравнений приходится иметь дело практически во всех разделах высшей математики. Сначала немного теории. Что в данном случае обозначает математическое слово «линейных»? Это значит, что в уравнения системы все переменные входят в первой степени . без всяких причудливых вещей вроде и т.п. от которых в восторге бывают только участники математических олимпиад. В высшей математике для обозначения переменных используются не только знакомые с детства буквы . Довольно популярный вариант – переменные с индексами: . Либо начальные буквы латинского алфавита, маленькие и большие: Не так уж редко можно встретить греческие буквы: – известные многим «альфа, бета, гамма». А также набор с индексами, скажем, с буквой «мю»: Использование того или иного набора букв зависит от раздела высшей математики, в котором мы сталкиваемся с системой линейных уравнений. Так, например, в системах линейных уравнений, встречающихся при решении интегралов, дифференциальных уравнений традиционно принято использовать обозначения Но как бы ни обозначались переменные, принципы, методы и способы решения системы линейных уравнений от этого не меняются. Таким образом, если Вам встретится что-нибудь страшное типа , не спешите в страхе закрывать задачник, в конце-концов, вместо можно нарисовать солнце, вместо – птичку, а вместо – рожицу (преподавателя). И, как ни смешно, систему линейных уравнений с данными обозначениями тоже можно решить. Что-то у меня есть такое предчувствие, что статья получится довольно длинной, поэтому небольшое оглавление. Итак, последовательный «разбор полётов» будет таким:: – Решение системы линейных уравнений методом подстановки («школьный метод») – Решение системы методом почленного сложения (вычитания) уравнений системы С системами линейных уравнений все знакомы из школьного курса математики. По сути дела, начинаем с повторения. Данный метод также можно назвать «школьным методом» или методом исключения неизвестных. Образно говоря, его еще можно назвать «недоделанным методом Гаусса». Пример 1 Решить систему линейных уравнений: Здесь у нас дана система из двух уравнений с двумя неизвестными. Обратите внимание, что свободные члены (числа 5 и 7) расположены в левой части уравнения. Вообще говоря, без разницы, где они находятся, слева или справа, просто в задачах по высшей математике нередко они расположены именно так. И такая запись не должна приводить в замешательство, при необходимости систему всегда можно записать «как обычно»: . Не забываем, что при переносе слагаемого из части в часть у него нужно поменять знак. Что значит решить систему линейных уравнений? Решить систему уравнений – это значит найти множество её решений. Решение системы представляет собой набор значений всех входящих в неё переменных, который обращает КАЖДОЕ уравнение системы в верное равенство. Кроме того, система может быть несовместной (не иметь решений) . Не тушуйтесь, это общее определение =) У нас же будет всего лишь одно значение «икс» и одно значение «игрек», которые удовлетворяют каждому уравнению с-мы. Существует графический метод решения системы, с которым можно ознакомиться на уроке Простейшие задачи с прямой . Там же я рассказал о геометрическом смысле системы двух линейных уравнений с двумя неизвестными. Но сейчас на дворе эра алгебры, и числа-числа, действия-действия. Решаем . из первого уравнения выразим: Полученное выражение подставляем во второе уравнение: Раскрываем скобки, приводим подобные слагаемые и находим значение : Далее вспоминаем про то, от чего плясали: Значение нам уже известно, осталось найти: Ответ . После того, как решена ЛЮБАЯ система уравнений ЛЮБЫМ способом, настоятельно рекомендую выполнить проверку (устно, на черновике либо калькуляторе) . Благо, делается это легко и быстро. 1) Подставляем найденный ответ в первое уравнение : – получено верное равенство. 2) Подставляем найденный ответ во второе уравнение : – получено верное равенство. Или, если говорить проще, «всё сошлось» Рассмотренный способ решения не является единственным, из первого уравнения можно было выразить , а не . Можно наоборот – что-нибудь выразить из второго уравнения и подставить в первое уравнение. Кстати, заметьте, самый невыгодный из четырех способов – выразить из второго уравнения: Получаются дроби, а оно зачем? Есть более рациональное решение. Тем не менее, в ряде случаев без дробей всё-таки не обойтись. В этой связи обращаю Ваше внимание на то, КАК я записал выражение. Не так: , и ни в коем случае не так: . Если в высшей математике Вы имеете дело с дробными числами, то все вычисления старайтесь проводить в обыкновенных неправильных дробях . Именно , а не или ! Запятую можно использовать лишь иногда, в частности, если – это окончательный ответ какой-нибудь задачи, и с этим числом больше не нужно выполнять никаких действий. Многие читатели наверняка подумали «да зачем такое подробное объяснение, как для класса коррекции, и так всё понятно». Ничего подобного, вроде бы такой простой школьный пример, а сколько ОЧЕНЬ важных выводов! Вот еще один: Любое задание следует стремиться выполнить самым рациональным способом . Хотя бы потому, что это экономит время и нервы, а также снижает вероятность допустить ошибку. Если в задаче по высшей математике Вам встретилась система двух линейных уравнений с двумя неизвестными, то всегда можно использовать метод подстановки (если не указано, что систему нужно решить другим методом) Ни один преподаватель не Более того, в ряде случаев метод подстановки целесообразно использовать и при большем количестве переменных. Пример 2 Решить систему линейных уравнений с тремя неизвестными Похожая система уравнений часто возникает при использовании так называемого метода неопределенных коэффициентов, когда мы находим интеграл от дробно-рациональной функции. Рассматриваемая система взята мной как раз оттуда. При нахождении интеграла – цель быстро найти значения коэффициентов , а не изощряться формулами Крамера, методом обратной матрицы и т.д. Поэтому, в данном случае уместен именно метод подстановки. Когда дана любая система уравнений, в первую очередь желательно выяснить, а нельзя ли ее как-нибудь СРАЗУ упростить? Анализируя уравнения системы, замечаем, что второе уравнение системы можно разделить на 2, что мы и делаем: Справка: математический знак обозначает «из этого следует это», он часто используется в ходе решения задач. Теперь анализируем уравнения, нам нужно выразить какую-нибудь переменную через остальные. Какое уравнение выбрать? Наверное, Вы уже догадались, что проще всего для этой цели взять первое уравнение системы: Здесь без разницы, какую переменную выражать, можно было с таким же успехом выразить или . Далее, выражение для подставляем во второе и третье уравнения системы: Раскрываем скобки и приводим подобные слагаемые: Третье уравнение делим на 2: Из второго уравнения выразим и подставим в третьей уравнение: Практически всё готово, из третьего уравнения находим: Из второго уравнения: Из первого уравнения: Ответ: Проверка: Подставим найденные значения переменных в левую часть каждого уравнения системы: 1) 2) 3) Получены соответствующие правые части уравнений, таким образом, решение найдено верно. Решить систему линейных уравнений с 4 неизвестными В ходе решения систем линейных уравнений нужно стараться использовать не «школьный метод», а метод почленного сложения (вычитания) уравнений системы. Почему? Это экономит время и упрощает вычисления, впрочем, сейчас станет всё понятнее. Пример 4 Решить систему линейных уравнений: Я взял ту же систему, что и первом примере. Анализируя систему уравнений, замечаем, что коэффициенты при переменной одинаковы по модулю и противоположны по знаку (–1 и 1). В такой ситуации уравнения можно сложить почленно: Действия, обведенные красным цветом, выполняются МЫСЛЕННО. Как видите, в результате почленного сложения у нас пропала переменная . В этом, собственно, и состоит суть метода – избавиться от одной из переменных . Теперь всё просто: – подставляем в первое уравнение системы (можно и во второе, но это не так выгодно – там числа больше): В чистовом оформлении решение должно выглядеть примерно так: Ответ: У некоторых явно возник вопрос: «Зачем все эти изыски, если можно просто выразить одну переменную через другую и подставить во второе уравнение?». Пример 5 Решить систему линейных уравнений: В данном примере можно использовать «школьный» метод, но большой минус состоит в том, что когда мы будем выражать какую-либо переменную из любого уравнения, то получим решение в обыкновенных дробях. А возня с дробями займет время, к тому же, если у Вас не «набита рука» на действиях с дробями, то велика вероятность допустить ошибку. Поэтому целесообразно использовать почленное сложение (вычитание) уравнений. Анализируем коэффициенты при соответствующих переменных: Как видим числа в парах (3 и 4), (4 и –3) – разные, поэтому, если сложить (вычесть) уравнения прямо сейчас, то от переменной мы не избавимся. Таким образом, хотелось бы видеть в одной из пар одинаковые по модулю числа, например, 20 и 20 либо 20 и –20. Будем рассматривать коэффициенты при переменной : Подбираем такое число, которое делилось бы и на 3 и на 4, причем оно должно быть как можно меньше. В математике такое число называется наименьшим общим кратным . Если Вы затрудняетесь с подбором, то можно просто перемножить коэффициенты: Далее: Первое уравнение умножаем на Второе уравнение умножаем на В результате: Вот теперь из первого уравнения почленно вычитаем второе . На всякий случай привожу еще раз действия, которые проводятся мысленно: Следует отметить, что можно было бы наоборот – из второго уравнения вычесть первое, это ничего не меняет. Теперь подставляем найденное значение в какое-нибудь из уравнений системы, например, в первое: Ответ: Решим систему другим способом. Рассмотрим коэффициенты при переменной Очевидно, что вместо пары коэффициентов (4 и –3) нам нужно получить 12 и –12. Для этого первое уравнение умножаем на 3, второе уравнение умножаем на 4: Почленно складываем уравнения и находим значения переменных: Решение системы линейных алгебраических уравнений методом Крамера Для проверки ответов можете воспользоваться нашим онлайн сервисом - Решение системы линейных уравнений методом Крамера. Если после изучения примеров решения задач у Вас останутся вопросы, то Вы всегда можете задать их на форуме. и не забывайте про наши онлайн калькуляторы для решения задач по математике и другим предметам! Систему уравнений можно представить в матричной форме: Ax = B, где А - основная матрица (квадратная матрица), В - матрица свободных членов. Теперь необходимо найти 4 определителя: определитель основной матрицы (определитель системы) и 3 определителя дополнительных матриц. Перед нахождением определителей советуем ознакомиться с теорией определителей матриц. а для нахождения определителей советуем использовать нашу программу - нахождение определителя матрицы. Перепишем систему линейных алгебраических уравнений в матричную форму . Слева от разделительной линии стоят коэффициенты при переменных, а справа стоят свободные члены. Уравнение может содержать не одну, а две переменных. Понятно, что такие уравнения называются уравнениями с двумя переменными . Система уравнений – это два и более уравнений, которыми можно манипулировать для нахождения общих решений. Система из двух уравнений вкючает в себя две переменных, значения которых являются общими для обоих уравнений. С помощью одного уравнения системы решается другое, а в итоге решаются оба уравнения системы. Суть в том, что в системе уравнений выбираете наиболее простое, в котором одну переменную выражаете через другую. Результат подставляете во второе уравнение, благодаря чему преобразуете его в более простое уравнение с одной переменной. Вычисляете это уравнение и получаете значение одной из переменных. Подставляется его в первое уравнение и получаете значение второй переменной. Так вы решаете всю систему уравнений. Пример. Решим систему уравнений │x + y = 1 │2x – y = 2 Решение : Первое уравнение системы проще второго – его и используем. Источники: 26 декабря 2024 годаПример решения системы линейных уравнений методом Гаусса
Как решить систему линейных уравнений?
Решение системы линейных уравнений методом подстановки
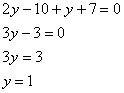
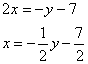
подумает, что ты лох снизит оценку за использование «школьного метода».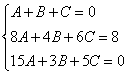
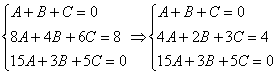
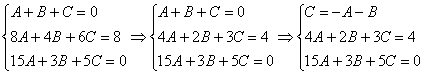
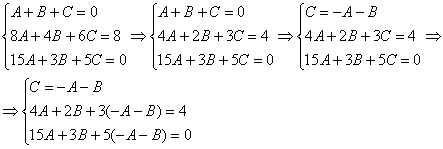
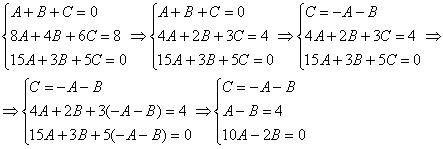
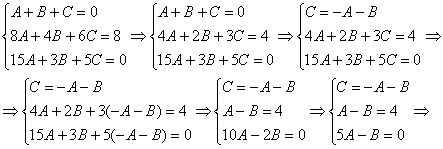
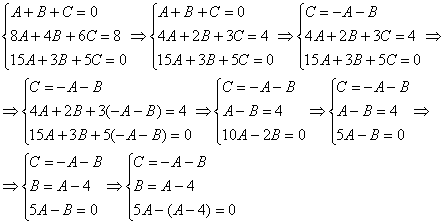
Решение системы методом почленного сложения (вычитания) уравнений системы
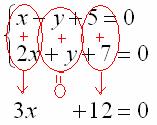
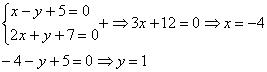
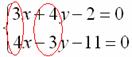
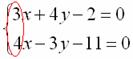
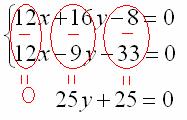
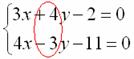
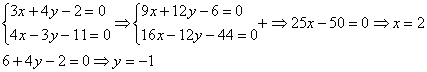
Решение СЛАУ 3-его порядка методом Крамера, пример № 1
Система уравнений с двумя переменными. Уравнения первой степени. Способы решения
, , , , Следующие документы
Другие статьи:
Популярное
Договор аренды с правом субаренды образец
(64) просмотров
Письмо вызов образец
(4) просмотров
Образец доверенности на трактор
(4) просмотров
Образец решения гск
(4) просмотров
Образец характеристики в прокуратуру
(3) просмотровНедавно добавленные материалы:

Как заполнить документы на субсидию
До 15 апреля и до 1 ноября этого года, предприятия, которые предоставляют услуги по газоснабжению, электроснабжению и
Какая помощь положена молодой семье на строительство дома?
1. Решение о предоставлении субсидии принимает уполномоченный орган исполнительной власти города Москвы.2. На основании решения о предоставлении уполномоченным органом исполнительной власти
Комментарий к Указу № 322 О предоставлении безналичных жилищных субсидий
29 августа 2016 годаПрезидент Беларуси Александр Лукашенко 29 августа подписал Указ № 322 «О предоставлении безналичных жилищных субсидий».Документом предусматривается внедрение
Конкурсный отбор по предоставлению субсидий начинающим предпринимателям
Министерство экономического развития Республики Ингушетия объявляет прием документов с 19 по 30 октября 2015 года, для участия
Как получить жилищные субсидии на приобретение жилья военнослужащим
Новости по тематикеСогласно федеральному закону «О статусе военнослужащих» № 76-ФЗ в редакции от 14.12.2015, государство берет на себя дополнительную ответственность за


 Характеристика опекаемой семьи образец
Характеристика опекаемой семьи образец Образец протокола собрания собственников многоквартирного дома
Образец протокола собрания собственников многоквартирного дома Образец заполнения декларации 3 ндфл для ип
Образец заполнения декларации 3 ндфл для ип Нотариально заверенная доверенность образец
Нотариально заверенная доверенность образец