Образцы решений уравнений

45. Примеры решения уравнений

Задача. Каждую сторону квадратной площадки увеличили на 2 метра, при этом ее площадь увеличилась на 12 квадратных метров. Чему была равна сторона площадки?

Решим эту задачу составлением уравнения.

Пусть x — длина (в метрах) стороны площадки тогда площадь этой площадки будет равна x 2 .

После того как сторону увеличили на 2 метра, получилась квадратная площадка со стороной (x + 2) метров, а площадь стала равной (x + 2) 2 квадратным метрам. Значит, площадь увеличилась на (x + 2) 2 – x 2 квадратных метров но по условию увеличение площади равно 12 кв. м, значит,

(x + 2) 2 – x 2 = 12

Мы получили уравнение. Чтобы его решить, сначала упростим левую часть. Применим формулу квадрата суммы:

(x + 2) 2 – x 2 = x 2 + 4x + 4 – x 2 = 4x + 4 .

Значит, уравнение можно записать так:

4x + 4 = 12 .

Находим 4x (как неизвестное слагаемое):

4 x = 8 и, наконец, x = 2.

При решении получившегося уравнения мы сперва упростили его левую часть.

Во многих случаях, преобразовав сначала выражения, содержащиеся в уравнении, можно упростить это уравнение и привести его к такому виду, который мы уже умеем решать.

Вычтем из первого произведения второе и перепишем левую часть уравнения в следующем виде: 2 x – 6.

Значит, данное уравнение (1) запишется так:

2 x – 6 = 2.

Это уравнение мы сможем решить. Найдем сначала 2x (как неизвестное уменьшаемое):

Примеры решения уравнений

Теория по уравнениям

ОПРЕДЕЛЕНИЕ

Уравнением называется равенство двух алгебраических выражений, в состав которых входят переменные.

Значение переменных, которое обращает уравнение в истинное равенство, называются решениями или корнями уравнения. Уравнение может иметь одно решение, несколько решений, бесконечное множество решений или не иметь решений вовсе. Уравнения называют равносильными, если любое решение первого являются решением и второго и наоборот.

Примеры

Решение

ОДЗ:

Разложим на множители знаменатели всех дробей:

Общий знаменатель этих дробей . Приведем дроби к общему знаменателю:

Далее числитель приравняем к нулю

Решим полученное квадратное уравнение, для этого вычислим дискриминант

корни квадратного уравнения

Оба корня входят в область допустимых значений.

Примеры решений дифференциальных уравнений

Решаем дифференциальное уравнение:

Произведем нормировку уравнения. Разделим все уравнение на коэффициент при y' . Получим:

Вычисляем вспомогательную фунцию:

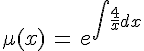образцы решений уравнений Вычисляем:

Согласно теории по данному типу диффуров, записываем выражение:

Интегрируем левую и правую часть. Получим:

Выразим искомую функцию y(x) :

Записываем финальный ответ .

Выполним проверку. Подставим полученную функцию y(x) в исходный диффур. Упрощаем:

Значение правой части диффура:

Выражения должны быть математически идентичны (с точностью до формы записи).

Решаем дифференциальное уравнение:

Произведем нормировку уравнения. Разделим все уравнение на коэффициент при y' . Получим:

Разделим все уравнение на y 2. Получили:

Делаем замену переменных.

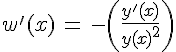образцы решений уравнений Тогда уравнение можно записать как:

Получили линейное неоднородное уравнение первого порядка . Решим его.

Решаем дифференциальное уравнение:

Вычисляем вспомогательную фунцию:

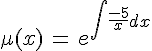образцы решений уравнений Вычисляем:

Согласно теории по данному типу диффуров, записываем выражение:

Интегрируем левую и правую часть. Получим:

Выразим искомую функцию w(x) :

Записываем решение уравнения:

Записываем финальный ответ .

Выполним проверку. Подставим полученную функцию y(x) в исходный диффур. 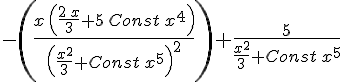образцы решений уравнений Упрощаем:

Выражение, записанное выше, это то, что получится при подстановке y(x) в левую часть диффура.

А теперь посмотрим что получится при подстановки y(x) в правую часть диффура:

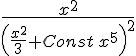образцы решений уравнений Упрощаем:

Выражения должны быть математически идентичны (с точностью до формы записи).

Решаем дифферениальное уравнение:

Упростим выражение, собрав коэффициенты при dx и dy .

Обозначим через P(x,y) коэффициент при dx

Обозначим через Q(x,y) коэффициент при dy

Проверяем равенство:

Равенство (2) выполняеться, значит уравнение (1) - это уравнение в полных дифференциалах

Ответ ищем в виде функции :

Предварительный ответ уже получили, надо найти функцию

Вспоминаем, что:

где

образцы решений уравнений

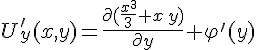
Запишем равенство (3) в явном виде

Выразим функцию

Примеры решения дифференциальных уравнений

Обыкновенные дифференциальные уравнения

Определение. Дифференциальным уравнением называется уравнение, связывающее независимые переменные, их функции и производные (или дифференциалы) этой функции.

Определение. Если дифференциальное уравнение имеет одну независимую переменную, то оно называется обыкновенным дифференциальным уравнением . если же независимых переменных две или более, то такое дифференциальное уравнение называется дифференциальным уравнением в частных производных.

Свойства общего решения

Дифференциальные уравнения первого порядка Определение. Дифференциальным уравнением первого порядка называется соотношение, связывающее функцию, ее первую производную и независимую переменную, т.е. соотношение вида:

Уравнения с разделяющимися переменными

Пример. Найти общее решение дифференциального уравнения:

Пример. Решить уравнение

Однородные уравнения Определение. Функция f ( x. y ) называется однородной n – го измерения относительно своих аргументов х и у, если для любого значения параметра t (кроме нуля) выполняется тождество:

Пример. Решить уравнение .

Уравнения, приводящиеся к однородным

Пример. Решить уравнение

Линейные уравнения Определение. Дифференциальное уравнение называется линейным относительно неизвестной функции и ее производной, если оно может быть записано в виде:

Линейные неоднородные дифференциальные уравнения

Метод Лагранжа

Пример. Решить уравнение

Уравнения в полных дифференциалах

Определение. Дифференциальное уравнение первого порядка вида:

называется уравнением в полных дифференциалах . если левая часть этого уравнения представляет собой полный дифференциал некоторой функции

Пример Решить уравнение

Уравнения Лагранжа и Клеро

Пример. Решить уравнение с заданными начальными условиями.

Пример. Найти общий интеграл уравнения .

Пример. Решить предыдущий пример другим способом.

Пример. Решить уравнение с начальным условием у(0) = 0.

Пример. Решить дифференциальное уравнение с начальным условием у(1) = 0.

Пример. Решить дифференциальное уравнение с начальным условием у(1)=0.

Геометрическая интерпретация решений дифференциальных уравнений первого порядка

Численные методы решения дифференциальных уравнений

Дифференциальные уравнения высших порядков

Уравнения, допускающие понижение порядка

Уравнения, не содержащие явно искомой функции и ее производных до порядка k – 1 включительно

Уравнения, не содержащие явно независимой переменной

Линейные дифференциальные уравнения высших порядков

Линейные однородные дифференциальные уравнения с произвольными коэффициентами

Структура общего решения

Общее решение линейного однородного дифференциального уравнения второго порядка

Линейные однородные дифференциальные уравнения с постоянными коэффициентами

Пример. Решить уравнение .

Пример. Решить уравнение

Линейные неоднородные дифференциальные уравнения с произвольными коэффициентами

Метод вариации произвольных постоянных

Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами

Уравнения с правой частью специального вида

Пример. Решить уравнение

Нормальные системы обыкновенных дифференциальных уравнений

Нормальные системы линейных однородных дифференциальных уравнений с постоянными коэффициентами

Пример. Найти решение системы уравнений

Пример. Найти общее решение системы уравнений:

Элементы теории устойчивости

Ляпунов Александр Михайлович

Классификация точек покоя

Классификация основных типов уравнений математической физики

Уравнения математической физики. Уравнения в частных производных.

Волновое уравнение

Уравнение колебаний струны

краевые условия

Решение задачи Коши методом разделения переменных.

Решение задачи Коши методом Даламбера

Уравнение теплопроводности

Уравнение Лапласа

Решение задачи Дирихле для круга

Ряды. Основные определения. Определение. Сумма членов бесконечной числовой последовательности называется числовым рядом .

Свойства рядов

Критерий Коши необходимые и достаточные условия сходимости ряда

Ряды с неотрицательными членами

Признак Коши. (радикальный признак) Если для ряда с неотрицательными членами существует такое число q <1, что для всех достаточно больших n выполняется неравенство то ряд сходится, если же для всех достаточно больших n выполняется неравенство

Пример. Определить сходимость ряда .

Интегральный признак Коши

Знакопеременные ряды. Знакочередующиеся ряды

Знакочередующийся ряд можно записать в виде: где

Признаки Даламбера и Коши для знакопеременных рядов

Функциональные последовательности Определение. Если членами ряда будут не числа, а функции от х. то ряд называется функциональным .

Функциональные ряды

Признак равномерной сходимости Вейерштрасса

Степенные ряды Определение. Степенным рядом называется ряд вида .

Теоремы Абеля

Действия со степенными рядами

Разложение функций в степенные ряды. Разложение функций в степенной ряд имеет большое значение для решения различных задач исследования функций, дифференцирования, интегрирования, решения дифференциальных уравнений, вычисления пределов, вычисления приближенных значений функции.

Способ разложения функции в ряд при помощи интегрирования

Пример. Разложить в степенной ряд функцию .

Решение дифференциальных уравнений с помощью степенных рядов С помощью степенных рядов возможно интегрировать дифференциальные уравнения.

Пример. Найти решение уравнения c начальными условиями y (0)=1, y ’(0)=0.

Ряды Фурье

Достаточные признаки разложимости в ряд Фурье

Ряд Фурье для четных и нечетных функций

Ряды Фурье для функций любого периода

Ряд Фурье по ортогональной системе функций Определение. Функции j (х) и y (х), определенные на отрезке [ a. b ], называются ортогональными на этом отрезке, если

Интеграл Фурье

Преобразование Фурье

Элементы теории функций комплексного переменного Определение. Если каждому комплексному числу z из некоторого множества D по некоторому закону поставлено в соответствие определенное комплексное число w из множества G. то на этой области задана однозначная функция комплексного переменного . отображающая множество D на множество G.

Производная функций комплексного переменного Определение. Производной от однозначной функции w = f ( z ) в точке z называется предел:

7. Уравнения и системы уравнений

чт, 05/25/2006 - 21:11 — admin

Уравнения и системы уравнений

Решение уравнений

Многие математические задачи сводятся к решению в общем случае нелинейных уравнений вида f(x) = 0 или f(x) = expr.

В системе Mathematica они обозначаются как eqns (от слова equations — уравнения). Разумеется, могут решаться и системы, состоящие из ряда таких уравнений.

Для решения уравнений (как одиночных, так и систем) в численном и символьном виде Mathematica имеет функцию Solve:

Solve [eqns, vars] — предпринимает попытку решить уравнение или систему уравнений eqns относительно переменных vars

Solve [eqns, vars, elims] — пытается решать уравнения eqns по переменным vars, исключая переменные elims.

Входные параметры этой функции могут быть представлены списками или записаны выражениями через объединительный знак«&&». В eqns в качестве знака равенства используется знак «= =». Примеры применения функции Solve представлены на рис. 4.12.

Рис. 4.12. Примеры решения уравнений

Обратите внимание на то, что в определенных ситуациях система подсказывает тонкости решения, выдавая предупреждающие сообщения. Если такие ситуации не являются ошибками, препятствующими решению, то полученное решение выводится в ячейку вывода.

Решение систем нелинейных уравнений в символьном виде

Приведенные на рис. 4.13 примеры показывают решение систем нелинейных уравнений с помощью функции Solve.

Достаточно характерен пример с применением функции N. Если убрать в нем функцию N, то будет получен чрезвычайно громоздкий, хотя и точный результат (проверьте это сами, поскольку размеры результата делают нецелесообразным его приведение в книге). Функция N осуществляет выполнение всех промежуточных вычислений, благодаря чему результат получается вполне обозримым и представленным в комплексных числах.

В последнем примере рис. 4.13 получен набор из пяти пар корней, определенных через функцию Root. Эта функция, в свою очередь, означает вычисление корней полиномиального уравнения пятой степени. Данный пример, как и ранее приводимые решения кубического уравнения, является наглядной иллюстрацией того, что простота нелинейных уравнений порой оказывается весьма обманчивой, а их решение порой приводит к весьма громоздким и сложным результатам. Тем не менее, возможность решения отдельных нелинейных уравнений и их систем в символьном виде трудно переоценить. К сожалению, далеко не все уравнения имеют такие решения — многие можно решать только в численном виде.

Рис. 4.13. Примеры решения систем нелинейных уравнений

Не следует полагать, что Mathematica всегда выдает верное решение систем нелинейных уравнений. На самом деле решение иногда бывает ошибочным. Поэтому в большинстве случаев стоит оформлять решение таким образом, чтобы обеспечить его проверку. Для этого рекомендуется отдельно задать систему уравнений и результат решения. Тогда проверка легко осуществляется с помощью подстановки. Два примера решения систем уравнений с проверкой решений показаны на рис. 4.14.

В первом примере решение кажется очевидным (равенства выполняются, например, при х=2 и у=3). Однако здесь Mathematica дает сразу три пары решений, и все они оказываются верны, поскольку после подстановки проверка всех равенств возвращает True.

А вот во втором примере проверка дала не совсем обычный результат, что связано с наличием в решении неопределенной переменной а. В таких случаях стоит попробовать упростить решение с помощью функции Simplify, что и показано на рис. 4.14.

Рис. 4.14. Примеры решения уравнений с проверкой

Опции функции Solve

С функцией Solve можно использовать ряд опций. Их можно вывести командой Options [Solve]. Ниже описано их назначение:

InverseFunctions — указывает, следует ли использовать обратные функции

MakeRules — указывает, должен ли результат быть представлен как объект AlgebraicRulesData

Method — устанавливает алгоритм, используемый для вычисления результата (возможны методы 1, 2 и 3)

Mode — задает характер решения уравнения (возможны Generic, Modular и Rational)

Sort — устанавливает, нужна ли сортировка результатов

Verif ySolutions — устанавливает, следует ли проводить проверку полученных решений и удаление посторонних решений

WorkingPrecision — устанавливает число цифр промежуточных вычислений (по умолчанию Infinity).

На рис. 4.15 приведены примеры применения функции Solve с опцией Inverse-Functions.

Обратите внимание на то, что последняя система уравнений при отсутствии опции InverseFunctions решается с предупреждением. Она вообще не решается, если эта опция задана как False, и гладко решается при InverseFunctions -> True.

Рис. 4.15. Примеры решения уравнений с опцией InverseFunction

То, насколько может влиять на решение опция Method, наглядно показывают примеры, представленные на рис. 4.16.

Рис. 4.16. Примеры решения уравнений разными методами

Множество примеров решения систем нелинейных уравнений в символьном виде можно найти в справочной системе Mathematica.

Численное решение уравнений

Многие нелинейные уравнения и системы нелинейных уравнений в принципе не имеют аналитических решений. Однако их решение вполне возможно численными методами. Для численного решения систем нелинейных уравнений используется функция NSolve:

NSolve [eqns, vars] — пытается численно решить одно уравнение или систему уравнений eqns относительно переменных vars

NSolve [eqns, vars, elims] — пытается численно решить уравнения eqns относительно vars, исключая переменные elims.

С этой функцией используется единственная опция WorkingPrecision, задающая число верных цифр результата — по умолчанию 16. На рис. 4.17 представлены примеры использования функции NSolve для численного решения уравнений.

Риc. 4.17. Примеры численного решения уравнений

Результаты решения с помощью функции NSolve также рекомендуется проверять с помощью подстановки, например, так:

е=2*х^2 + 5*х- 15 == х^3

-15 + 5х + 2х2 ==х3

r=NSolve[e,x]

Нетрудно заметить, что в данном случае решение верно.

Источники:
mthm.ru, ru.solverbook.com, diffurov.net, fislub.ru, lib.qrz.ru