Образцы решения злп симплексным методом
Планирование решений в экономике
Добро пожаловать на наш портал !
Методы компьютерного моделирования экономических процессов
Пример решения ЗЛП симплекс-методом
Пример решения ЗЛП симплекс-методом . Рассмотрим на конкретном примере процесс решения КЗЛП табличным симплекс-методом. Пусть дана каноническая задача ЛП:
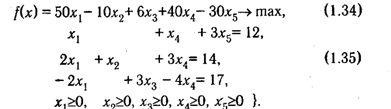
Как видно, столбцы матрицы с номерами <5, 2, 3> являются линейно независимыми. И можно получить разложение по данным столбцам вектора ограничений с положительными коэффициентами. Последнее означает, что столбцы <5, 2, 3> образуют допустимый базис, с которого можно начать решение задачи. Из столбцов, входящих в базис, с учетом нулевых элементов формируется матрица ( (1) ) и обратная по отношению к ней -1 ( (1) ):
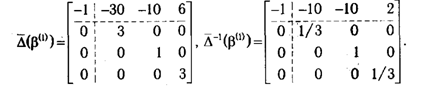
Используя их, по формуле (1.26) получаем
Пример - Табличный симплекс метод
Необходимо решить задачу линейного программирования.
Целевая функция:
Ограничивающие условия:
Приведем систему ограничений к каноническому виду, для этого необходимо перейти от неравенств к равенствам, с добавлением дополнительных переменных.
Так как наша задача - задача минимизации, то нам необходимо преобразовать ее к задаче на поиск максимума. Для этого изменим знаки коэффициентов целевой функции на противоположные. Элементы первого неравенства записываем без изменений, добавив в него дополнительную переменную x5 и изменив знак ≤ на =. Т. к. второе и третье неравенства имеют знаки ≥ необходимо поменять знаки их коэффициентов на противоположные и внести в них дополнительные переменные x6 и x7 соответственно. В результате получем эквивалентную задачу:
Переходим к формированию исходной симплекс таблицы. В строку F таблицы заносятся коэффициенты целевой функции с противоположным знаком.
Пример решения задачи линейного программирования симплекс-методом.
Симплекс-метод решения задачи линейного программирования.
Рассмотрим однородную задачу ЛП из примера №1 п. 1.5.:
(1)
Добавив к левым частям системы неравенств соответствующие балансовые переменные преобразуем задачу (1) в каноническую форму:
Для удобства и единообразия запишем определение целевой функции в виде уравнения:
(3)
Запишем (2) и (3) в виде первой симплекс таблицы:
Пример решения прямой и двойственной задачи симплекс методом
Рассмотрен пример решения задачи симплекс методом, а также пример решения двойственной задачи.
Условие задачи
Для реализации трех групп товаров коммерческое предприятие располагает тремя видами ограниченных материально-денежных ресурсов в количестве b1 = 240, b2 = 200, b3 = 160 единиц. При этом для продажи 1 группы товаров на 1 тыс. руб. товарооборота расходуется ресурса первого вида в количестве a11 = 2 единицы, ресурса второго вида в количестве a21 = 4 единицы, ресурса третьего вида в количестве a31 = 4 единицы. Для продажи 2 и 3 групп товаров на 1 тыс. руб. товарооборота расходуется соответственно ресурса первого вида в количестве a12 = 3, a13 = 6 единицы, ресурса второго вида в количестве a22 = 2, a23 = 4 единицы, ресурса третьего вида в количестве a32 = 6, a33 = 8 единиц. Прибыль от продажи трех групп товаров на 1 тыс. руб. товарооборота составляет соответственно c1 = 4, c2 = 5, c3 = 4 (тыс. руб.). Определить плановый объем и структуру товарооборота так, чтобы прибыль торгового предприятия была максимальной.
К прямой задаче планирования товарооборота, решаемой симплекс методом . составить двойственную задачу линейного программирования.
Согласно сопряженным парам переменных из решения прямой задачи получить решение двойственной задачи . в которой производится оценка ресурсов . затраченных на продажу товаров.
Решение задачи симплекс методом
Решаем симплекс методом.
Вводим дополнительные переменные x4 &ge 0, x5 &ge 0, x6 &ge 0, чтобы неравенства преобразовать в равенства.
Данные заносим в симплекс таблицу
Симплекс таблица № 1
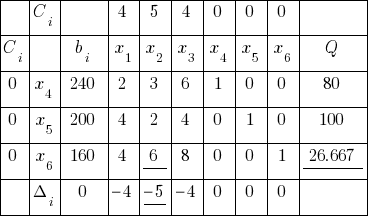
Целевая функция:
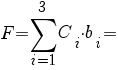 0 · 240 + 0 · 200 + 0 · 160 = 0
0 · 240 + 0 · 200 + 0 · 160 = 0
Вычисляем оценки по формуле:
&Delta2 = 0 · 3 + 0 · 2 + 0 · 6 - 5 = - 5
&Delta3 = 0 · 6 + 0 · 4 + 0 · 8 - 4 = - 4
&Delta4 = 0 · 1 + 0 · 0 + 0 · 0 - 0 = 0
&Delta5 = 0 · 0 + 0 · 1 + 0 · 0 - 0 = 0
&Delta6 = 0 · 0 + 0 · 0 + 0 · 1 - 0 = 0
Поскольку есть отрицательные оценки, то план не оптимален. Наименьшая оценка:
Вводим переменную x2 в базис.
Определяем переменную, выходящую из базиса. Для этого находим наименьшее неотрицательное отношение 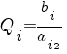 для столбца x2 .
для столбца x2 .
Из 1-й строки вычитаем 3-ю строку, умноженную на 3
Из 2-й строки вычитаем 3-ю строку, умноженную на 2
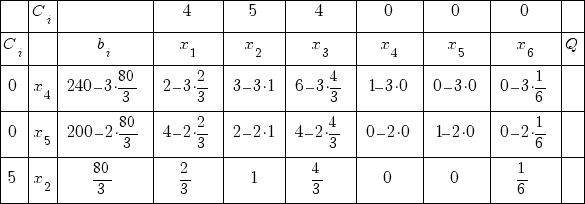
Получаем новую таблицу:
Симплекс таблица № 2
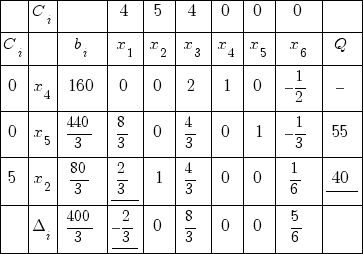
Целевая функция:
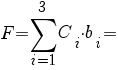 0 · 160 + 0 · 440/3 + 5 · 80/3 = 400/3
0 · 160 + 0 · 440/3 + 5 · 80/3 = 400/3
Вычисляем оценки по формуле:
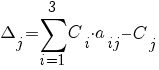
&Delta1 = 0 · 0 + 0 · 8/3 + 5 · 2/3 - 4 = - 2/3
&Delta2 = 0 · 0 + 0 · 0 + 5 · 1 - 5 = 0
&Delta3 = 0 · 2 + 0 · 4/3 + 5 · 4/3 - 4 = 8/3
&Delta4 = 0 · 1 + 0 · 0 + 5 · 0 - 0 = 0
&Delta5 = 0 · 0 + 0 · 1 + 5 · 0 - 0 = 0
&Delta6 = 0 · (-1)/2 + 0 · (-1)/3 + 5 · 1/6 - 0 = 5/6
Поскольку есть отрицательная оценка &Delta1 = - 2/3, то план не оптимален.
Вводим переменную x1 в базис.
Определяем переменную, выходящую из базиса. Для этого находим наименьшее неотрицательное отношение 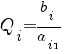 для столбца x1 .
для столбца x1 .
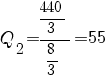
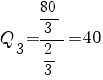
Наименьшее неотрицательное: Q3 = 40. Выводим переменную x2 из базиса
3-ю строку делим на 2/3.
Из 2-й строки вычитаем 3-ю строку, умноженную на 8/3
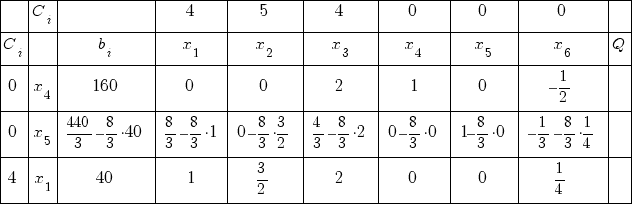
Получаем новую таблицу:
Симплекс таблица № 3
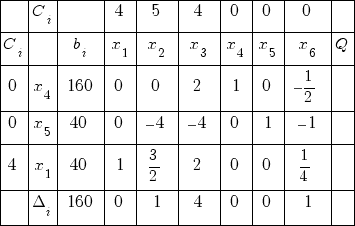
Целевая функция:
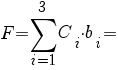 0 · 160 + 0 · 40 + 4 · 40 = 160
0 · 160 + 0 · 40 + 4 · 40 = 160
Вычисляем оценки по формуле:
&Delta6 = 0 · (-1)/2 + 0 · (-1) + 4 · 1/4 - 0 = 1
Ответ
Решение двойственной задачи
Пример решения задачи линейного программирования симплексным методом
Задача. Для изготовления различных изделий A и B используется 2 вида сырья. На производство единицы изделия A его требуется затратить: 1-го вида -15кг, 2-го вида - 11кг, 3-го вида - 9кг. На производство единицы изделия B требуется затратить сырья 1-го вида - 4кг, 2-го вида - 5кг, 3-го вида - 10кг.
Производство обеспечено сырьем 1-го вида в количестве 1095кг, 2-го вида - 865кг, 3-го вида -1080кг.
Прибыль от реализации единицы готового изделия А составляет 3 рубля, изделия B - 2 рубля. Составить план производства изделий А и В, обеспечивающий максимальную прибыль от их реализации.
Решение. Составим задачу линейного программирования
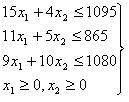
Приведем к канонической форме
Источники:
, , , ,
Следующие документы
27 декабря 2024 года
Комментарии: 1
Другие статьи:
Популярное
Договор аренды с правом субаренды образец
(126) просмотров
Образец решения об объединение комнат в квартиру
(9) просмотров
Образец доверенности на трактор
(6) просмотров
Характеристика сантехника с места работы образец
(6) просмотров
Образец решения гск
(6) просмотровНедавно добавленные материалы:

Как заполнить документы на субсидию
До 15 апреля и до 1 ноября этого года, предприятия, которые предоставляют услуги по газоснабжению, электроснабжению и
Какая помощь положена молодой семье на строительство дома?
1. Решение о предоставлении субсидии принимает уполномоченный орган исполнительной власти города Москвы.2. На основании решения о предоставлении уполномоченным органом исполнительной власти
Комментарий к Указу № 322 О предоставлении безналичных жилищных субсидий
29 августа 2016 годаПрезидент Беларуси Александр Лукашенко 29 августа подписал Указ № 322 «О предоставлении безналичных жилищных субсидий».Документом предусматривается внедрение
Конкурсный отбор по предоставлению субсидий начинающим предпринимателям
Министерство экономического развития Республики Ингушетия объявляет прием документов с 19 по 30 октября 2015 года, для участия
Как получить жилищные субсидии на приобретение жилья военнослужащим
Новости по тематикеСогласно федеральному закону «О статусе военнослужащих» № 76-ФЗ в редакции от 14.12.2015, государство берет на себя дополнительную ответственность за


 Преамбула дополнительному договору образец
Преамбула дополнительному договору образец Протест на решение суда образец
Протест на решение суда образец Образец договора с иностранцем
Образец договора с иностранцем Акт ввода прибора учета в эксплуатацию образец
Акт ввода прибора учета в эксплуатацию образец Письмо ответ отказ образец
Письмо ответ отказ образец Образцы писем на украинском языке
Образцы писем на украинском языке Образец договора продажи газопровода
Образец договора продажи газопровода